AMPLIFICADORES OPERACIONALES.
Son circuitos integrados con un nivel de componentes y
estructura interna complicada por lo que los vamos a estudiar
Son circuitos integrados con un nivel de componentes y
estructura interna complicada por lo que los vamos a estudiar
desde fuera como cajas negras. Su símbolo es el siguiente:
La alimentación del circuito se realiza por medio de dos fuentes
de alimentación (alimentación simétrica).Como se aprecia en la siguiente figura, el terminal de referencia de tensiones (masa) no está
conectado directamente al amplificador operacional. La
referencia de tensiones debe realizarse a través de elementos
externos al operacional tales como resistencias.
Tienen dos entradas la "-" que se denomina “inversora” y la "+" que
se denomina “no inversora” y una salida Vo. Se alimentan a
través de dos terminales uno con tensión positiva +V y otro con
tensión negativa -V. Adicionalmente pueden tener otros
terminales específicos para compensación de frecuencia,
corrección de derivas de corriente continua etc.
Se encuentran integrados de forma que en una pastilla puede
haber 1, 2 ó 4 OP (amplificadores operacionales). En el caso de
4 el número de patillas mínimo es 3x4(I/O)+2(alim)=14. Son muy
baratos (más que muchos transistores).
Existen varios modelos de OP. Vamos a estudiar en primer lugar
el IDEAL. Es un modelo simplificado que se adapta bien al
comportamiento real. Sin embargo a veces necesitaremos
aproximarnos más con lo que describiremos el modelo REAL que es
el ideal más una serie de imperfecciones.
se denomina “no inversora” y una salida Vo. Se alimentan a
través de dos terminales uno con tensión positiva +V y otro con
tensión negativa -V. Adicionalmente pueden tener otros
terminales específicos para compensación de frecuencia,
corrección de derivas de corriente continua etc.
Se encuentran integrados de forma que en una pastilla puede
haber 1, 2 ó 4 OP (amplificadores operacionales). En el caso de
4 el número de patillas mínimo es 3x4(I/O)+2(alim)=14. Son muy
baratos (más que muchos transistores).
Existen varios modelos de OP. Vamos a estudiar en primer lugar
el IDEAL. Es un modelo simplificado que se adapta bien al
comportamiento real. Sin embargo a veces necesitaremos
aproximarnos más con lo que describiremos el modelo REAL que es
el ideal más una serie de imperfecciones.
AMPLIFICADOR OPERACIONAL IDEAL.
En el modelo de amplificador ideal, la salida del amplificador
se obtiene a través de la expresión:
Vo=A((V+)-(V-)= AVD
Esta expresión nos dice que la salida del amplificador es
directamente proporcional a la diferencia de potencial Vd en la
entrada. Designaremos a la constante de proporcionalidad A como
GANANCIA EN LAZO ABIERTO. Con esta definición podemos decir
también que el amplificador operacional es DIFERENCIAL ya que la
salida depende de la diferencia de tensión en sus entradas.
A es una constante para cada amplificador y sus valores son muy
altos (>200000 para amplificadores reales). En lazo abierto
significa que es la ganancia del propio dispositivo sin conectar
a nada.
Propiedades del amplificador operacional ideal
1. La ganancia en lazo abierto A es infinita
2. Las resistencias que se ven desde cada uno de los terminales
de entrada son infinitas o, lo que es lo mismo, las
intensidades de entrada I- e I+ son nulas.
3. La impedancia de carga de un circuito conectado en cascada con
el OP no influye en la tensión de salida: Vo≠ f (ZL). Esto
significa que, si tenemos el equivalente del amplificador de
la forma:
En el modelo de amplificador ideal, la salida del amplificador
se obtiene a través de la expresión:
Vo=A((V+)-(V-)= AVD
Esta expresión nos dice que la salida del amplificador es
directamente proporcional a la diferencia de potencial Vd en la
entrada. Designaremos a la constante de proporcionalidad A como
GANANCIA EN LAZO ABIERTO. Con esta definición podemos decir
también que el amplificador operacional es DIFERENCIAL ya que la
salida depende de la diferencia de tensión en sus entradas.
A es una constante para cada amplificador y sus valores son muy
altos (>200000 para amplificadores reales). En lazo abierto
significa que es la ganancia del propio dispositivo sin conectar
a nada.
Propiedades del amplificador operacional ideal
1. La ganancia en lazo abierto A es infinita
2. Las resistencias que se ven desde cada uno de los terminales
de entrada son infinitas o, lo que es lo mismo, las
intensidades de entrada I- e I+ son nulas.
3. La impedancia de carga de un circuito conectado en cascada con
el OP no influye en la tensión de salida: Vo≠ f (ZL). Esto
significa que, si tenemos el equivalente del amplificador de
la forma:
Por tanto para que se cumpla la condición de que Vo ≠ f (ZL) tiene
que ser Ro = 0es decir la impedancia de salida del OP es nula.
4. Es un amplificador de corriente continua y alterna
5. Es capaz de amplificar la señal de entrada independientemente
de su frecuencia. El ancho de banda es por tanto infinito.
Por la primera propiedad, tendríamos que si A es infinito como
Vd es un valor finito debería ser Vo infinito. Como esto no
puede ser debe ocurrir que Vd = 0 es decir V+ = V-
Las alimentaciones de un amplificador suelen ser iguales en
magnitud y tienen como valores típicos +/-5V, +/-9V, +/-12V, +/-
15V, +/-18V, +/-22V. La salida puede tener valores máximos algo
inferiores que las tensiones de alimentación. Por tanto se
elegirá la alimentación en función de las disponibilidades y de los niveles de señal necesarios en la salida del OP.
Los OP se suelen utilizar con realimentación ya que esto hace
que podamos controlar su ganancia. Como veremos la ganancia en
lazo cerrado no dependa nada más que del circuito externo
aplicado. Según como sea este circuito tendremos varias
configuraciones de amplificador.
AMPLIFICADOR INVERSOR
Vamos a calcular su ganancia en lazo cerrado G y su resistencia
de entrada Ri.
Como V+ está unida a tierra, será V− = 0 . Esto se conoce como
TIERRA VIRTUAL ya que está como conectada a tierra pero sin
estarlo.
I= Vin/R1
Vo= -R2/R1
Vo/Vi = -R2/R1= G
donde, por tanto, G puede ser mayor o menor que 1 sin más que
elegir las resistencias de la forma adecuada.
Ri= IR1/I = R1
AMPLIFICADOR NO INVERSOR
La resistencia de entrada se obtendra de la siguiente manera.
Ri = Vi/I = Vi/0= ∞
ya que por definición, en el modelo ideal la intensidad I=0.
En cuanto a la ganancia, sabemos que V- = V+ = Vi` , si suponemos que
por R1 pasa una intensidad I1 cuyo valor sería
I1= Vi / R1
la tensión Vo se obtendría
Vo= I1 (R1 + R2) = Vi/R1 ( R1 + R2)
La ganancia sera : G = Vo/Vi = (R1+R2)/R1 = 1+ R2/R1
Como se puede observar, en este caso, la ganancia será siempre
positiva ya que las Ri son siempre positivas y además siempre
será mayor o igual a 1.
Ri = Vi/I = Vi/0= ∞
ya que por definición, en el modelo ideal la intensidad I=0.
En cuanto a la ganancia, sabemos que V- = V+ = Vi` , si suponemos que
por R1 pasa una intensidad I1 cuyo valor sería
I1= Vi / R1
la tensión Vo se obtendría
Vo= I1 (R1 + R2) = Vi/R1 ( R1 + R2)
La ganancia sera : G = Vo/Vi = (R1+R2)/R1 = 1+ R2/R1
Como se puede observar, en este caso, la ganancia será siempre
positiva ya que las Ri son siempre positivas y además siempre
será mayor o igual a 1.
AMPLIFICADOR SUMADOR
La salida de este amplificador es proporcional a la suma de las
señales de entrada. Dado que V- =0 por ser igual a V+ que sí es
igual a cero, las intensidades que circulan por cada rama son
independientes de las demás y no se produce redistribución de
intensidad alguna. Con ello la intensidad total que atraviesa
R2 será la suma de las intensidades de cada una de las ramas de
entrada.
Haciendo que R1 = R1 = ..... = R1N = R4 se consigue que
Vo= -ΣVij
Lo normal sería obtener una suma ponderada de manera que a
cada término se le puede dar el peso que nos interese.
AMPLIFICADOR DIFERENCIAL
Se trata de una configuración con dos entradas, en la que se
amplifica la diferencia de potencial entre ambas. Para obtener
las expresiones correspondientes a esta configuración tendremos
en cuenta que su comportamiento es en todo momento lineal. Por
ello, aplicaremos el teorema de superposición. Primero
supondremos que una de las tensiones de entrada es nula y
obtendremos la salida correspondiente, a continuación supondremos que la otra tensión es nula y también
obtendremos la expresión de Vo, la solución completa se consigue mediante la
suma de ambas soluciones.
"Con esto ultimo pasemos a la practica para dar uso a esta teoria un tanto aburrida"
DESARROLLO DE LA PRACTICA
cuando la luz choca sobre el LDR el circuito se apaga:
cuando la luz choca sobre el LDR el circuito se apaga:
En cuanto comienza a disminuir la luminisodad sobre el LDR la lamparita enciende:
en el siguiente video se pueden observar el modo de calibracion, el funcionamiento del circuito, y el desperfecto total de los alumnos jajaja.
En la experiencia del fotocontrol, podremos verificar el funcionamiento del LM741 (amplificador
operacional), en la configuracion de ampificador diferencial. Tambien usaremos un LDR (light depending
resistor) que consiste en un sensor de luz que al recivir mucha luz, su resistencia disminiye. Y cuando recibe
muy poca luz su resistencia aumenta. a continuador detallamos el conexionado del fotocontrol y sus
vistas en plaquetas y en protoboard:
operacional), en la configuracion de ampificador diferencial. Tambien usaremos un LDR (light depending
resistor) que consiste en un sensor de luz que al recivir mucha luz, su resistencia disminiye. Y cuando recibe
muy poca luz su resistencia aumenta. a continuador detallamos el conexionado del fotocontrol y sus
vistas en plaquetas y en protoboard:
(Circuito eléctrico del fotocontrol)
(simulacion en una plaqueta utilizando el programa pcb wizard)
Con esto podemos dar por terminado el tema “amplificador operacional” i pasar al tema que nos ocupara en lo siguiente “filtros”
"FILTROS"
El consepto de filtro en la electronica talvez no sea el que nosotros tenemos de los filtros, en los circuitos electronicos y especialmente en los de audio se intenta obtener una señal “limpia” por llamarla asi de algun modo, esto se complica dependiendo del circuito dado que todos los circuitos tienen senales indeseadas de diferentes tipos como perturbaciones, distorcion, ruido etc.
Pero el capitulo que veremos a continuación tomara como tema principal la discriminación de frecuencias. Ya que si debemos definir en pocas palabras a un filtro se podria decir que es “un circuito electronico que discrimina frecuencias o una gama de ellas que pasan por el, es decir las diferencia por ser de baja media o alta frecuencia” podiendo a partir de esto elegir con cual o desde que rango o valor hasta otro trabajar, para entender este concepto explicaremos a que se llama ancho de banda. Por ejemplo en el sig grafico se toma una señal cualquiera (azul) y el rango representado entre F1 y F2 es el ancho de banda.
Este consepto tiene una gran cantidad de aplicaciones pero aviendo entendido esto sigamos con los filtros.
repitamos nuevamente la definición de filtro:
“un circuito electronico que discrimina frecuencias o una gama de ellas que pasan por el, es decir las diferencia por ser de baja media o alta frecuencia”
Vamos entonces los principales tipos de filtros y sus caracteristicas:
Filtros pasa bajos, pasa altos, pasa banda y elimina banda:
Según su respuesta en frecuencia, los filtros se pueden clasificar básicamente en cuatro categorías diferentes:
Filtro pasa bajos: Son aquellos que introducen muy poca atenuación a las frecuencias que son menores que una determinada, llamada frecuencia de corte. Las frecuencias que son mayores que la de corte son atenuadas fuertemente.
Existe un símbolo para cada uno de estos filtros, símbolo que se usa en los diagramas de bloques de los aparatos electrónicos. Estos símbolos son los siguientes:
Filtro pasa altos: Este tipo de filtro atenúa levemente las frecuencias que son mayores que la frecuencia de corte e introducen mucha atenuación a las que son menores que dicha frecuencia.
Filtro pasa banda: En este filtro existen dos frecuencias de corte, una inferior y otra superior. Este filtro sólo atenúa grandemente las señales cuya frecuencia sea menor que la frecuencia de corte inferior o aquellas de frecuencia superior a la frecuencia de corte superior. por tanto, sólo permiten el paso de un rango o banda de frecuencias sin atenuar.
Filtro elimina banda: Este filtro elimina en su salida todas las señales que tengan una frecuencia comprendida entre una frecuencia de corte inferior y otra de corte superior. Por tanto, estos filtros eliminan una banda completa de frecuencias de las introducidas en su entrada.
Algunas definiciones más:
Son una definiciones muy sencillas pero necesarias:
Octava: Dos frecuencias están separadas una octava si una de ellas es de valor doble que la otra.
Década: Dos frecuencias están separadas una década si una de ellas es de valor diez veces mayor que la otra.
Frecuencia de corte: Es la frecuencia para la que la ganancia en tensión del filtro cae de 1 a 0.707 (esto expresado en decibelios, dB, se diría como que la ganancia del filtro se reduce en 3dB de la máxima, que se considera como nivel de 0dB). En los filtros pasa banda y elimina banda existirán dos frecuencias de corte diferentes, la inferior y la superior.
Banda de paso: Es el rango de frecuencias que el filtro deja pasar desde la entrada hasta su salida con una atenuación máxima de 3dB. Toda frecuencia que sufra una atenuación mayor quedaría fuera de la banda pasante o de paso.
Banda atenuada: Es el rango de frecuencias que el filtro atenúa más de 3dB.
Orden del filtro: De forma sencilla se podría definir así,
Filtro de primer orden: atenúa 6dB/octava fuera de la banda de paso.
Filtro de segundo orden: atenúa 12dB/octava fuera de la banda de paso.
Filtro de tercer orden: atenúa 18dB/octava fuera de la banda de paso.
Filtro de orden n: atenúa (6n)dB/octava fuera de la banda de paso.
El filtro pasa bajos:
Los circuitos usados como filtros de primer orden de tipo pasivo son los siguientes:
Quizás el más usado es el primero de ellos, ya que no suele ser fácil conseguir bobinas con las características deseadas.
El funcionamiento de estos circitos como filtro pasa bajos es fácil de entender. En el caso del primero, el condensador presentará una gran oposición al paso de corrientes debidas a frecuencias bajas y como forma un divisor de tensión con la resistencia, aparecerá sobre él casi toda la tensión de entrada. Para frecuencias altas el condensador presentará poca oposición al paso de la corriente y la resistencia se quedará casi el total de la tensión de entrada, apareciendo muy poca tensión en extremos del condensador. El segundo circuito funcionará de forma muy parecida al primero. Aquí también tenemos un divisor de tensión formado por al bobina y la resistencia. Si la frecuencia de la tensión de entrada es baja la bobina ofrecerá poca oposición y la tensión caerá casi toda ella en la resistencia (o sea, aparecerá en la salida). Si la frecuencia de la señal de entrada es alta la bobina se quedará en sus extremos con casi toda la tensión y no aparecerá casi ninguna en la salida.
Efectuemos el estudio de este tipo de filtros sobre el primero de ellos, el que tiene un condensador y una resistencia. La ganancia en tensión del filtro será
Para el caso de que la frecuencia de entrada coincida con fc tendremos pues que la ganancia del filtro quedaría como
El círculo se ha cerrado y, por tanto, las dos definiciones de la frecuencia de corte son equivalentes.
Expresando Gv en función de la frecuencia tendremos que:
Si representamos gráficamente Gv obtenemos lo siguiente:
La misma representación gráfica pero con Gv expresada en decibelios tiene el siguiente aspecto:
Como puede apreciarse en esta última representación, cada vez que la frecuencia se dobla la ganancia cae -6db (aproximadamente). Es esta una característica de los filtros de primer orden: la ganancia cae -6db por octava fuera de la banda de paso.
Los filtros, además de afectar a la amplitud de la señal que se les introduce en función de su frecuencia, también afectan o modifican la fase de las señales, y dicha modificación también será una u otra en función de la frecuencia de la señal de entrada. Veamos cómo se produce este efecto. El desfase entre la tensión en extremos del condensador (tensión de salida) y la tensión aplicada en la entrada vendrá dado por:
ste ángulo saldrá negativo indicando que la tensión de salida estará atrasada respecto a la de entrada.
Representando gráficamente la expresión anterior del desfase tendremos lo siguiente:
Si el eje de frecuencias lo representamos logarítmicamente la gráfica tendrá el siguiente aspecto:
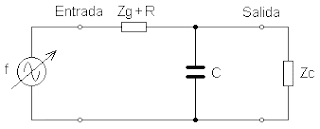
Hasta aquí todo muy bien, todo muy bonito. Pero, el filtro deberá conectar su entrada y su salida a "algo". El funcionamiento descrito más arriba sería el de un filtro conectado a una fuente de señal con impedancia nula (algo que en la práctica no pasa) y con la salida abierta (¿y entonces para qué quiero un filtro?). Lo que tendremos en la realidad sera algo como lo siguiente:
¿Como afectan Zg y Zc al funcionamiento del filtro? Restrinjamos el estudio a los casos en que tanto Zg como Zc sólo tengan componente real, o sea, sean de tipo exclusivamente resistivo. Lo normal es que Zg sea pequeña o muy pequeña, con lo que no tendría apenas influencia sobre el funcionamiento del filtro. De todas formas, si se desea considerar su efecto, sólo hay que ver que queda en serie con la resistencia del filtro, con lo que el filtro que se obtendría sería el siguiente:
El círculo se ha cerrado y, por tanto, las dos definiciones de la frecuencia de corte son equivalentes.
Expresando Gv en función de la frecuencia tendremos que:
Si representamos gráficamente Gv obtenemos lo siguiente:
La misma representación gráfica pero con Gv expresada en decibelios tiene el siguiente aspecto:
Como puede apreciarse en esta última representación, cada vez que la frecuencia se dobla la ganancia cae -6db (aproximadamente). Es esta una característica de los filtros de primer orden: la ganancia cae -6db por octava fuera de la banda de paso.
Los filtros, además de afectar a la amplitud de la señal que se les introduce en función de su frecuencia, también afectan o modifican la fase de las señales, y dicha modificación también será una u otra en función de la frecuencia de la señal de entrada. Veamos cómo se produce este efecto. El desfase entre la tensión en extremos del condensador (tensión de salida) y la tensión aplicada en la entrada vendrá dado por:
ste ángulo saldrá negativo indicando que la tensión de salida estará atrasada respecto a la de entrada.
Representando gráficamente la expresión anterior del desfase tendremos lo siguiente:
Si el eje de frecuencias lo representamos logarítmicamente la gráfica tendrá el siguiente aspecto:
Hasta aquí todo muy bien, todo muy bonito. Pero, el filtro deberá conectar su entrada y su salida a "algo". El funcionamiento descrito más arriba sería el de un filtro conectado a una fuente de señal con impedancia nula (algo que en la práctica no pasa) y con la salida abierta (¿y entonces para qué quiero un filtro?). Lo que tendremos en la realidad sera algo como lo siguiente:
¿Como afectan Zg y Zc al funcionamiento del filtro? Restrinjamos el estudio a los casos en que tanto Zg como Zc sólo tengan componente real, o sea, sean de tipo exclusivamente resistivo. Lo normal es que Zg sea pequeña o muy pequeña, con lo que no tendría apenas influencia sobre el funcionamiento del filtro. De todas formas, si se desea considerar su efecto, sólo hay que ver que queda en serie con la resistencia del filtro, con lo que el filtro que se obtendría sería el siguiente:
Por tanto, para el cálculo de un filtro teniendo en cuenta el efecto de Zg, de carácter puramente resistivo, sólo hay que considerar como resistencia del filtro el valor de Zg + R (con lo que la fuente de señal pasaría a considerarse como perfecta, esto es, con una impedancia cero -ya que su impedancia ha pasado a formar parte de la resistencia del filtro-).
En cuanto al efecto introducido por Zc, decir que si ésta es grande o muy grande comparada con el valor de Xc a la frecuencia fc se podrá despreciar su efecto (nos estaríamos acercando al caso de salida abierta, equivalente a resistencia infinita).
En cuanto al efecto introducido por Zc, decir que si ésta es grande o muy grande comparada con el valor de Xc a la frecuencia fc se podrá despreciar su efecto (nos estaríamos acercando al caso de salida abierta, equivalente a resistencia infinita).
El filtro pasa alto:
Podemos implementar un filtro de estas características mediante alguno de los siguientes circuitos:
En esta ocasión realizaremos el estudio sobre el filtro a base de bobina y resistencia. Empecemos por la ganancia en tensión:
Por otro lado, la frecuencia de corte (o sea, aquella para la que Xl = R) será:
Y el desfase entre la tensión de salida respecto la de entrada es:
Se puede ver que este filtro adelanta la tensión de salida respecto a la de entrada.
Las representaciones gráficas correspondientes a este tipo de filtro serían las siguientes:
Las representaciones gráficas correspondientes a este tipo de filtro serían las siguientes:
Se puede apreciar la pendiente de -6dB/octava en la banda atenuada del filtro.
Consideraciones sobre la impedancia de la fuente de señal y sobre la impedancia que se conecte a la salida del filtro se podrán aplicar a este filtro igual que ya se hizo en el filtro pasa bajos.
El filtro pasa banda:
Se puede conseguir un filtro paso banda conectando en cascada (uno tras otro) un filtro pasa altos y un filtro pasa bajos:
La respuesta en frecuencia que cabe esperar de un filtro de este tipo será algo similar a esto:
Pues bien, la fci vendrá determinada por el filtro pasa altos y la fcs por el pasa bajos. Teniendo en cuenta esto y las fórmulas ya desarrolladas para ambos tipos de filtros (¿cómo, todavía no realizó el estudio para el pasa altos con condensado?) no es difícil su cálculo (aproximado) para una determinada banda de paso.
“Tanta teoria ya nos esta fritando el cerebro asi que dejemos de escribir tanto y pasemos al laboratorio a diseñar alguno de estos circuitos”.
circuito pasa bajos
circuito pasa bajos
filtro pasa altas
“Estos fueron algunos de los tantos circuitos que realizamos en el laboratorio de ELECTRONICA 2 del CUBA, hasta la próxima y esperamos que les aya sido de utilidad”
